Begriffe und Konzepte der Informatik: Bubblesort

Das einfachste Sortierverfahren

Über die drei einfachen Sortierverfahren Bubblesort, Selectionsort und Insertionsort wird auf dieser Homepage an mehreren Stellen geschrieben. Zum Thema Bubblesort gibt es zwei Seiten, eine für Schüler(innen) der gymnasialen Oberstufe, eine für Studierende der Informatik und Wirtschaftsinformatik im ersten Semester.

Der Bubblesort ist nicht unbedingt das einfachste der drei einfachen Sortierverfahren, meiner Meinung nach ist eigentlich der Selectionsort oder auch der Insertionsort einfacher zu verstehen. Der Bubblesort wird aber in den meisten Quellen als erstes Verfahren aufgelistet, weil er sich relativ einfach programmieren lässt.

Auf den Algorithmus des Verfahrens wollen wir auf dieser Seite nicht näher eingehen, das Thema wird auf den beiden oben verlinkten Seiten für Schüler(innen) und Studierende intensiv besprochen. Auf dieser Seite wollen wir uns auf das Zeitverhalten des Algorithmus konzentrieren.

Zeitverhalten des Bubblesort

Dazu führen wir folgendes Experiment durch. Wir ergänzen den Quelltext des Bubblesort-Algorithmus um ein paar Zeilen:

    public void bubblesortMitZaehlung()
    {
        int operationen = 0;

        for (int durchgang = 1; durchgang < MAX-1; durchgang++)
        {
            operationen += 3; // init, vergleich, inkrement
            for (int i=0; i < MAX-1; i++)
            {
                operationen += 3; // init, vergleich, inkrement

                if (zahlen[i] > zahlen[i+1])
                {
                    tauschen(i,i+1);
                    operationen += 4; // tauschen, vergleich
                }    
                else
                    operationen += 1; // nur vergleichen
            }        
        }    
        
        System.out.println("Für " + MAX + " Zahlen wurden "+ operationen + " Operationen benötigt.");
    }

Die Konstante MAX wurde in der Klasse definiert, in der sich diese modifizierte Methode befindet. Der Quelltext wurde so ergänzt, dass alle Vergleiche und Zuweisungen aufsummiert und am Ende ausgegeben werden.

Jeder Schleifendurchgang inkrementiert den Zähler operationen um 3, einmal für die Initialisierung der Laufvariable, dann für die Kontrolle der Schleifenbedingung und schließlich um das Inkrementieren der Laufvariable. Eigentlich sollte man nur beim ersten Schleifendurchgang um 3 inkrementieren und bei den folgenden Durchgängen um 2, denn die Laufvariable wir nur einmal initialisiert. Aber wie wir gleich noch sehen werden, spielt diese Überlegung im Grunde keine große Rolle.

Der Vergleich if (zahlen[i] > zahlen[i+1]) wird als eine weitere Operation gezählt, und wenn ein Tauschvorgang nötig ist, wird der Zähler um 3 inkrementiert, denn beim Tauschen werden ja drei Zuweisungen ausgeführt.

Diese Methode wurde für folgende MAX-Werte ausgeführt und protokolliert:

100 Zahlen 46623 Operationen.
200 Zahlen 187872 Operationen.
400 Zahlen 755862 Operationen.
800 Zahlen 3036087 Operationen.
1600 Zahlen 12113724 Operationen.

Nun ziehen wir die Quadratwurzel der Operationen-Zahl und kommen zu folgendem Ergebnis:

100 Zahlen 216² Operationen.
200 Zahlen 4332² Operationen.
400 Zahlen 8692² Operationen.
800 Zahlen 17422² Operationen.
1600 Zahlen 34802² Operationen.

Stellen wir das Ganze nun graphisch dar:

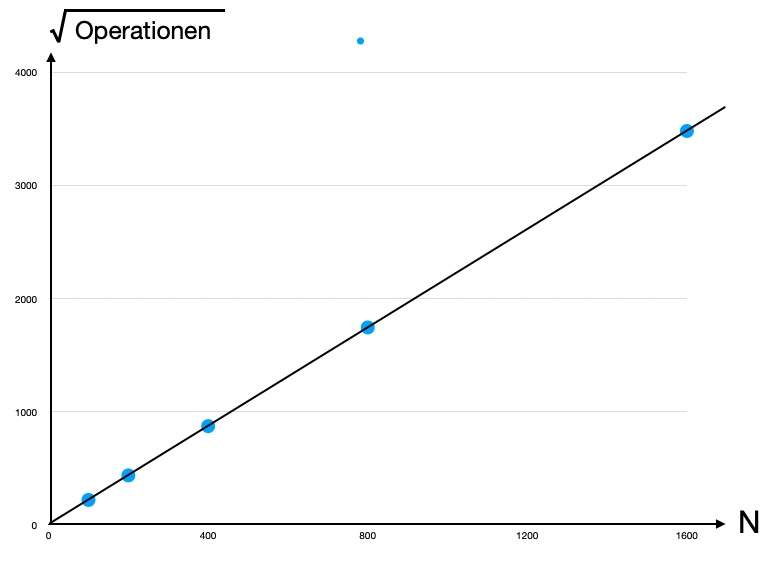
Zeitverhalten des Bubblesort - eigene Messung
Autor: Ulrich Helmich 11/2025, Lizenz: Public domain

Dieses Bild zeigt, dass die Rechenzeit des Algorithmus linear mit dem Quadrat von N ansteigt. Auf der X-Achse haben wir die Zahl der Elemente N, auf der Y-Achse die Quadratwurzel aus der Zahl der aussummierten Operationen. Es gilt für die Zahl der Operationen O:

O = k * N²

So schreibt man das in der Informatik allerdings nicht, sondern man verwendet die sogenannte O-Notation:

Zeitaufwand = O(N²).