Bäume allgemein
Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Unter einem Baum versteht man eine Datenstruktur, bei der jedes Element mindestens zwei Nachfolger hat. Diese Nachfolger können aber - mal wieder typisch für Mathematiker und Informatikerinnen - leer sein.
Hier eine interessante rekursive Definition aus einem alten Fachbuch; leider sind mir Titel und Autor nicht mehr verfügbar:
Baum
Ein Baum ist entweder leer oder besteht aus einem Baum mit mindestens zwei Nachfolgern.
Vier Bäume
Autor: Ulrich Helmich 2022, Lizenz: Public domain
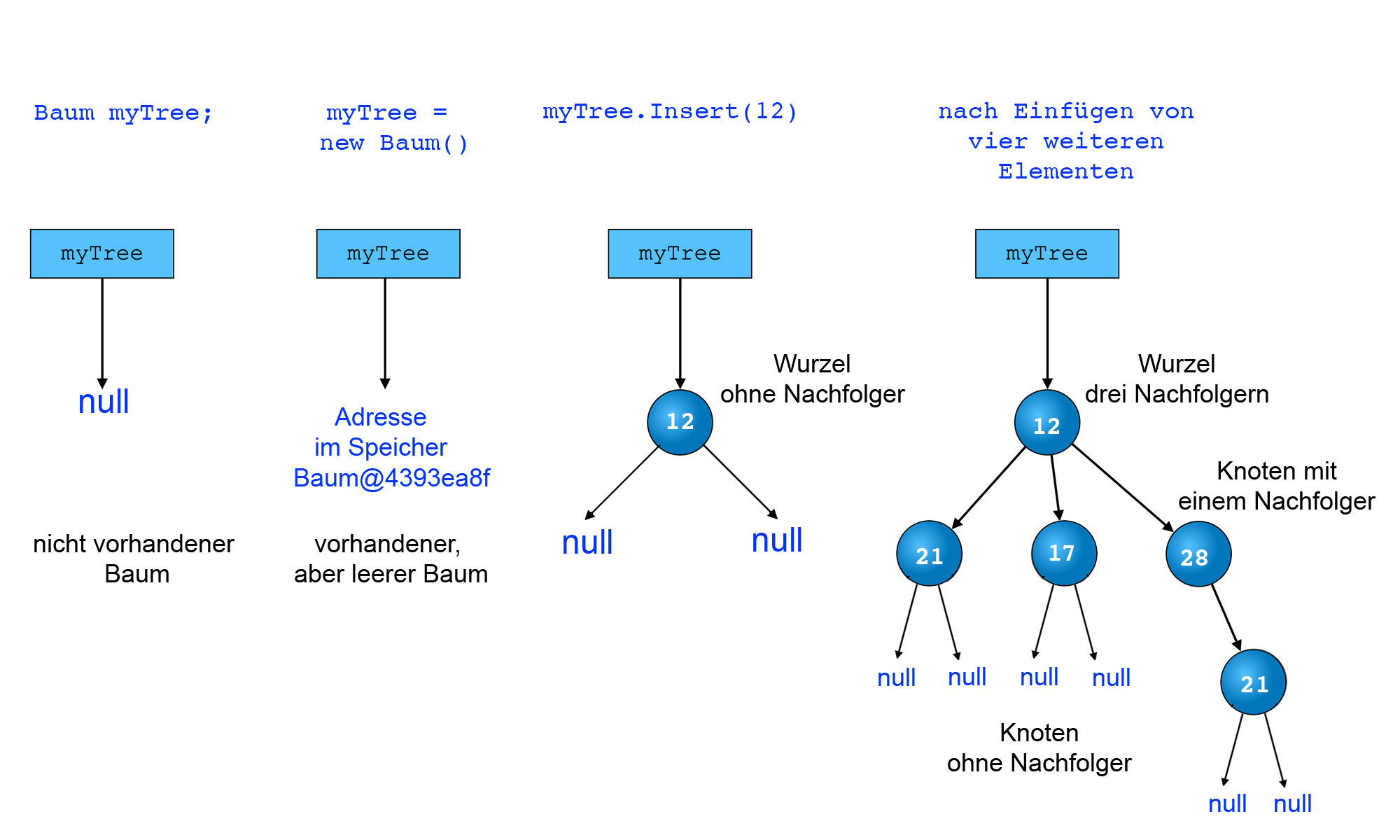
Angenommen, die Klasse Baum repräsentiert einen Baum. Nach der Deklaration
Baum myTree;
ist eine Instanzvariable myTree erzeugt worden, eine Referenzvariable, die aber noch keinen Wert hat, also quasi auf null zeigt.
Nach der Initialisierung
myTree = new Baum()
speichert die Instanzvariable myTree eine Speicheradresse. Der Baum an sich ist damit schon vorhanden, aber er ist noch leer. Es existiert keine Wurzel mit einem Eintrag.
Nach Aufruf von
myTree.Insert(12)
ist der Baum nicht mehr leer. Er besteht aus einer Wurzel und zwei noch nicht vorhandenen Nachfolger-Bäumen.
Laut Definition muss ein Baum, wenn er nicht leer ist, mindestens zwei Nachfolger haben, die aber leer sein können. Genau das wird in der Zeichnung oben dargestellt. Die Wurzel 12 hat zwei leere Nachfolger bzw. noch nicht existierende Nachfolger.
Hier könnte man jetzt darüber philosophieren, ob die Nachfolger-Zeiger der Wurzel einen vorhandenen leeren Baum abbilden oder einen nicht vorhandenen Baum repräsentieren (der nicht leer sein kann, weil er ja noch gar nicht existiert).
Wichtige Fachbegriffe
Wurzel = Das einzige Baum-Element, das keinen Vorgänger hat.
Blatt = Baum-Element, das keine bzw. nur leere Nachfolger hat.
Innerer Knoten = Baum-Element, das einen Vorgänger und mindestens einen nicht-leeren Nachfolger hat.
Höhe / Tiefe = maximale Zahl der Ebenen eines Baumes.
Kante = die Verbindung zwischen einem Vorgänger- und einem Nachfolgerknoten.
Pfad = die Folge der Kanten, die aufeinanderfolgende Knoten verbinden.
Niveau / Level = Länge des Pfades von der Wurzel zu einem Knoten.
Ordnung = maximale Zahl der Nachfolger, die ein Element haben kann.
Erläuterung der Fachbegriffe
Erläuterung der Fachbegriffe
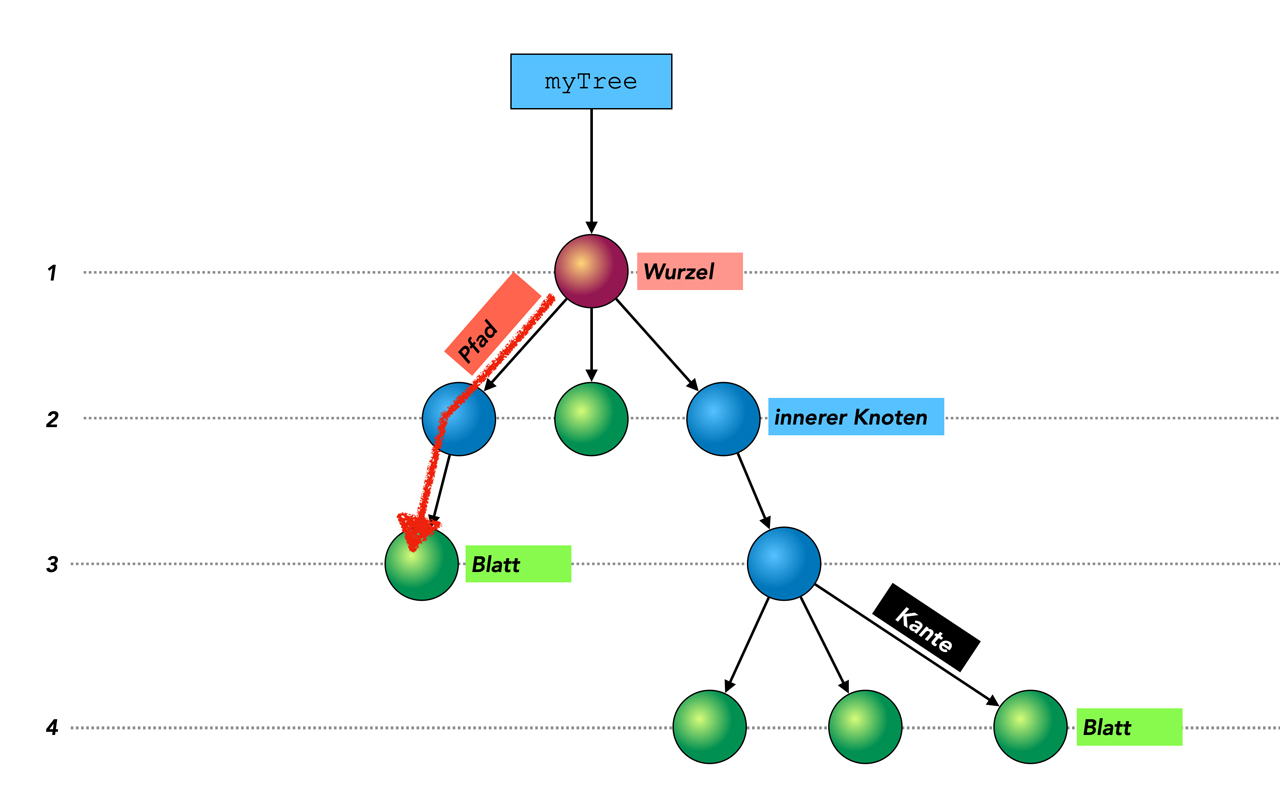
Die Graphik zeigt einen typischen Baum. Die Wurzel ist der rot gefärbte obere Knoten, die Blätter sind grün gefärbt und die inneren Knoten blau.
Die Höhe bzw. Tiefe des Baums beträgt 4, da der Baum aus vier Ebenen besteht.
Eine Kante ist in der Abbildung beschriftet, und ein Pfad ist durch einen dicken roten Pfeil markiert. Dieser Pfad führt von der Wurzel über den linken Nachfolger zu dessen linken (und einzigen) Nachfolger auf der Ebene 3. Das Niveau bzw. der Level dieses Pfades hat dann den Wert 2.
Die Ordnung dieses konkreten Baumes ist 3, denn kein Knoten hat mehr als drei Nachfolger.
Anwendungsbeispiele
Bäume werden auf vielfältige Weise in der Informatik genutzt, zum Beispiel als Stammbaum einer Familie, als Dateistruktur auf einer Festplatte, als Gliederung eines PDF-Dokuments, als Organisationsdiagramm, als Entscheidungsbaum bei einem Computerspiel und so weiter.
Baum-Typen
Geordneter Baum
Bei einem geordneten Baum sind die Nachfolger eines Knotens in einer bestimmten Reihenfolge angeordnet.
Binärbaum
Ein Baum, bei dem jeder Knoten maximal zwei Nachfolger hat.
Binärer Suchbaum
Ein Binärbaum, der gleichzeitig ein geordneter Baum ist. Weitere Einzelheiten siehe Folge 17.2 in dem Java-Kurs für die Stufe Q1/Q2.
Ausgeglichener Baum, AVL-Baum
Ein Baum, der möglichst viele Knoten auf einer Ebene enthält und bei dem die Pfade möglichst kurz sind. Weitere Einzelheiten siehe Folge 18.1 in dem Java-Kurs für die Q1/Q2.
B-Baum
Ein Baum, dessen Knoten aus geordneten Listen bestehen, wobei jedes Listenelement auf einen weiteren Nachfolger-Knoten zeigt. Weitere Einzelheiten siehe Folge 18.5 in dem Java-Kurs für die Q1/Q2.