Ein verblüffender Versuch
Wie immer auf dieser Homepage führen wir zunächst einen kleinen Versuch durch, und dann werden die Versuchsbeobachtungen ausführlich besprochen und erklärt.
Lesen Sie sich diese Seite gut durch, und kommen Sie dann hier wieder zurück...
Erläuterungen
Obwohl wir zwei fast identische Halbzellen miteinander verbunden haben, kann man deutlich eine Spannung ablesen - zwar nicht sehr groß, aber immerhin. Wo kommen die 0,06 Volt bzw. 0,12 V eigentlich her? Wir haben doch zwei gleiche Silber-Elektroden verwendet, nur die Konzentrationen der Silbernitrat-Lösungen unterscheiden sich um den Faktor 10 bzw. 100.
Betrachten wir die Gleichgewichtsreaktion, die innerhalb einer Silber-Halbzelle abläuft:
$Ag_{(s)} \rightleftharpoons Ag^{+}_{(aq)}+ e^{-}$
Falls der Browser die Formeln auf dieser Seite nicht richtig darstellt, wurde die Erweiterung MathJax nicht korrekt geladen. Entweder ist der Browser veraltet, oder es besteht im Augenblick keine Internetverbindung.
Das Gleichgewicht dieser Reaktion liegt weit auf der linken Seite, beim festen Silber Ag(s). Aber wie Sie sicherlich aus dem Unterricht der Jahrgangsstufe EF wissen, kann man chemische Gleichgewichte beeinflussen. Nach dem Le Chatelierschen Prinzip (Prinzip des kleinsten Zwanges) kann man ein Gleichgewicht nach rechts verschieben, indem man entweder die Konzentration der Edukte erhöht oder die Konzentration der Produkte vermindert.
Vergleichen wir nun die Gleichgewichtslagen der beiden Halbzellen.
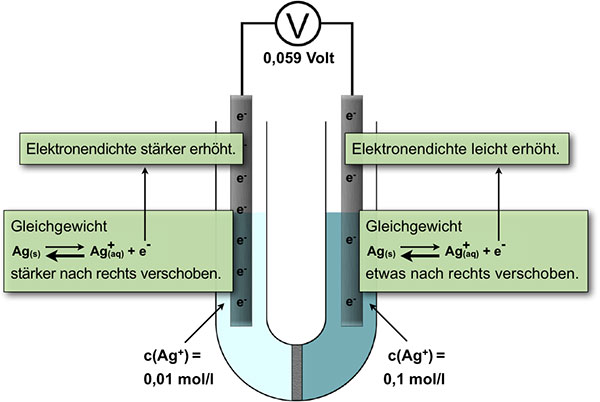
Chem. Gleichgewichte in einer Silber-Konzentrationszelle
Autor: Ulrich Helmich 2016, Lizenz: Public domain.
In der rechten Halbzelle mit der 0,1-molaren Silbernitrat-Lösung liegt das chemische Gleichgewicht auf der Eduktseite beim Ag(s).
In der linken Halbzelle mit der 0,01-molaren Silbernitrat-Lösung liegt das Gleichgewicht ebenfalls auf der Eduktseite, also beim Ag(s). Allerdings ist hier die Ag+-Konzentration um den Faktor 10 geringer als in der rechten Halbzelle. Die Produkt-Konzentration ist also verringert worden gegenüber der rechten Halbzelle.
Das Gleichgewicht der Reaktion wird in der linken Halbzelle (0,01-molar) also etwas stärker nach rechts verschoben als in der rechten Halbzelle (0,1-molar). Auch die freigesetzten Elektronen gehören zu den Produkten der Gleichgewichtsreaktion. Wenn in der linken Halbzelle mehr Ag+-Ionen entstehen, werden dort auch mehr Elektronen freigesetzt als in der rechten Halbzelle.
Spannung
Verbindet man die beiden Elektroden über ein Voltmeter, so ist klar, dass man eine Spannung misst, denn es liegt ja ein Ladungsunterschied vor: In der linken Elektrode befinden sich mehr Elektronen als in der rechten Elektrode. Daher können wir die linke Elektrode auch als Donator-Elektrode oder Minuspol bezeichnen, während die rechte Elektrode als Akzeptor-Elektrode oder Pluspol bezeichnet werden kann.
Merke:
Eine galvanische Zelle, die aus zwei gleichen Halbzellen aufgebaut ist, die sich nur durch die Konzentration des Elektrolyten unterscheiden, wird als Konzentrationszelle bezeichnet. In der Halbzelle mit der niedrigeren Elektrolytkonzentration werden Metall-Atome Me zu Metall-Kationen Men+ oxidiert (Donator-Halbzelle), in der Halbzelle mit der höheren Elektrolytkonzentration werden die gleichen Metall-Kationen zu Metall-Atomen reduziert (Akzeptor-Halbzelle).
Die NERNSTsche Gleichung
Kommen wir nun noch einmal auf die Ergebnisse des Versuchs zurück; hier eine tabellarische Darstellung der (idealen) Ergebnisse:
| c(Donator) in mol/L |
c(Akzeptor) in mol/L |
U in Volt |
| 0,1 | 0,1 | 0 |
| 0,01 | 0,1 | 0,059 |
| 0,001 | 0,1 | 0,118 |
| 0,0001 | 0,1 | 0,177 |
Dann erkennen wir leicht den Zusammenhang zwischen Spannung U und Konzentrationsdifferenz zwischen Donator-Halbzelle und Akzeptor-Halbzelle. Es gilt die folgende Gleichung, die auch als Nernst-Gleichung oder Nernstsche Gleichung bekannt geworden ist:
$U = \frac{0,059}{z} * lg \frac{c(Donator)}{c(Akzeptor)}$
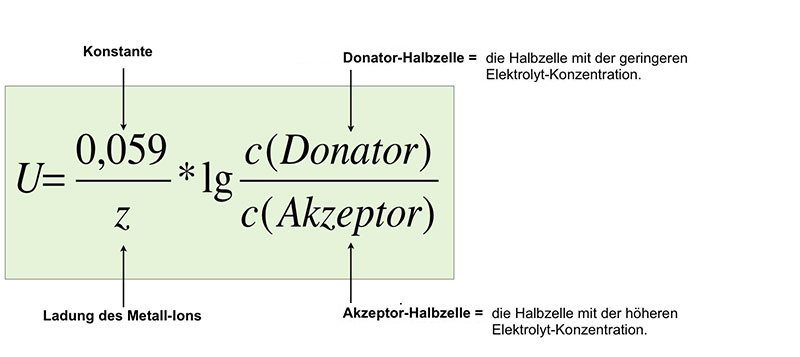
Erläuterung der Nernst-Gleichung
Autor: Ulrich Helmich 2016, Lizenz: Public domain.
Die Ladung des Metall-Ions beträgt bei Silberhalbzellen +1; die Gleichung vereinfacht sich dadurch etwas.
Rechnen wir nun einmal nach: In unserem Versuch beträgt c(Donator) = 0,01 mol/l und c(Akzeptor) = 0,1 mol/l. Der dekadische Logarithmus aus dem Quotienten dieser beiden Werte ist dann -1. Multipliziert mit dem Faktor 0,059/1 erhält man also eine Spannung von -0,059 Volt. Diesen Wert können wir bei dem Versuch allerdings nur dann messen, wenn er perfekt abläuft.
Aufgabe
Berechnen Sie die Spannung einer Silber-Konzentrationszelle mit c(Donator) = 0,05 mol/l und c(Akzeptor) = 0,8 mol/l.
Lösung:
Der dekadische Logarithmus aus dem Quotienten 0,05/0,8 ist -1,204. Wenn wir diesen Wert mit der Konstanten 0,059 multiplizieren erhalten wir eine Spannung von -0,071 Volt.
Konzentrationsabhängigkeit von Redoxpotenzialen
Nun gilt die Konzentrationsabhängigkeit des Redoxpotenzials bzw. Elektrodenpotenzials aber nicht nur für Konzentrationszellen, sondern grundsätzlich für alle galvanischen Elemente.
Rechenbeispiel 1
Das Redoxpotenzial von Zink beträgt -0,76 Volt. Das gilt aber nur dann, wenn die Zinkionen-Konzentration den Wert 1 mol/l hat und wenn auch sonst Standardbedingungen herrschen.
Wie wirkt sich jetzt eine Erhöhung der Zn2+-Konzentration auf 2 mol/l auf das Elektrodenpotenzial einer Zink-Halbzelle aus?
Erst mal mit dem gesunden Menschenverstand...
Bevor wir jetzt eine anspruchsvolle Berechnung durchführen, wollen wir zuerst einmal den gesunden Menschenverstand einschalten. Betrachten wir dazu die Redoxreaktion, die an der Grenzfläche zwischen der Zink-Elektrode und der Zinksulfat-Lösung abläuft:
$Zn_{(s)} \rightleftharpoons Zn^{2+}_{(aq)}+ 2 \ e^{-}$
Eine Erhöhung von c(Zn2+) "drückt" das chemische Gleichgewicht nach links, auf die Eduktseite. Es werden also weniger Zn2+-Ionen und damit auch weniger Elektronen freigesetzt als bei einer Standard-Zinkhalbzelle mit c(Zn2+) = 1 mol/l.
Auch Edelmetalle setzen weniger Elektronen frei als Zink, und deren Redoxpotenzial ist bekanntlich positiver als das von Zink. Man sollte also meinen, dass das Elektrodenpotenzial der Zink-Elektrode durch die Erhöhung der Zinkkonzentration etwas positiver wird.
... und jetzt mit der Nernst-Gleichung
Um das resultierende Elektrodenpotenzial zu berechnen, kann man folgende Form der NERNSTschen Gleichung verwenden:
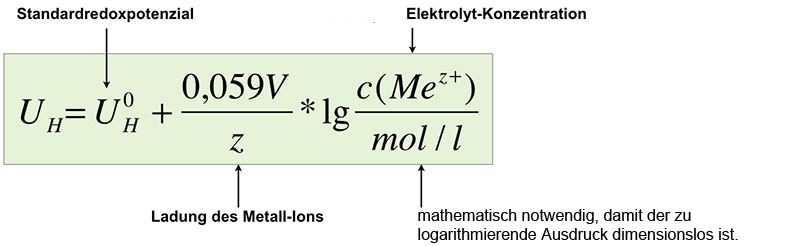
Die NERNST-Gleichung für Elektrodenpotenziale
Autor: Ulrich Helmich 2016, Lizenz: Public domain.
$U^{0}_{H}$ ist dabei das Standardredoxpotenzial des Metalls bzw. des Systems Me/Mez+. Bei einer Zink-Halbzelle müsste man hier also den Wert -0,76 V einsetzen.
Angenommen, die Konzentration der Zink-Ionen beträgt jetzt c(Zn2+) = 2,0 mol/l. Dann berechnet man den dekadischen Logarithmus von 2,0. Es ergibt sich der Wert 0,30.
Mit 0,059 multipliziert und durch 2 dividiert ergibt sich der Wert 0,0089 Volt, den man zum Standardredoxpotenzial hinzuaddieren muss. Das aktuelle Redoxpotenzial dieser Zink-Halbzelle hat dann den Wert -0,76 +0,0089 = -0,7511 Volt. Das Redoxpotenzial ist also durch die Erhöhung der Zink-Lösung etwas weniger negativ geworden.
Rechenbeispiel 2
Wie groß ist das Elektrodenpotenzial einer Kupferhalbzelle mit c(Cu2+) = 0,4 mol/l ?
Zunächst schlagen wir das Standardredoxpotenzial von Kupfer in einer Tabelle nach, dabei kommen wir auf den Wert +0,34 V. Dann ziehen wir den Logarithmus aus 0,4 und erhalten -0,398. Multipliziert mit 0,059V und dividiert durch 2 (z = 2) erhalten wir -0,0117 V. Diesen Wert addieren wir zu unseren +0,34 V und erhalten +0,328 Volt. Bei der Kupferhalbzelle wird das Redoxpotenzial etwas negativer, wenn wir die Elektrolytlösung verdünnen.
Rechenbeispiel 3
Wie kann man die Spannung einer Kupfer-Zink-Zelle erhöhen?
Wir müssen das Elektrodenpotenzial der Zink-Halbzelle erniedrigen (negativer machen), und das Elektrodenpotenzial der Kupferhalbzelle erhöhen (positiver machen).
Das chemische Gleichgewicht der Reaktion
$Zn_{(s)} \rightleftharpoons Zn^{2+}_{(aq)}+ 2 \ e^{-}$
ziehen wir auf die Seite mit den Elektronen (also auf die rechte Seite), indem wir c(Zn2+) erniedrigen. Die Zinksulfat-Lösung sollte also eine möglichst niedrige Konzentration haben, beispielsweise 0,01 mol/l.
Das chemische Gleichgewicht der Reaktion
$Cu_{(s)} \rightleftharpoons Cu^{2+}_{(aq)}+ 2 \ e^{-}$
ziehen wir auf die rechte Cu(s)-Seite, indem wir die Konzentration der Kupfersulfat-Lösung erhöhen. Die Löslichkeit von Kupfersulfat beträgt ca. 200 g pro Liter (wasserfreies Kupfersulfat). Das sind ca. 1,2 mol.
Für die Zinkhalbzelle erhalten wir dann ein Redoxpotenzial von -0,76 + 0,059/2 * lg(0,01) = -0,76 + 0,059/2 * -2 = -0,76 + -0,059 = -0,82 Volt.
Für die Kupferhalbzelle berechnet sich das Redoxpotenzial nach 0,34 + 0,059/2 * lg(1,2) = 0,34 + 0,0295 * 0,079 = 0,34 + 0,0023 = 0,3423 Volt.
Die Spannung, die unsere verbesserte Zink-Kupfer-Zelle liefert, liegt dann bei 1,1623 Volt. Das ist auch nicht viel mehr als die 1,1 Volt, die man unter Standardbedingungen erhält.