Das Würfel-Beispiel
Wie groß wird die Wahrscheinlichkeit sein, beim Würfeln mit drei Würfeln spontan einen geordneten Zustand herzustellen, z.B. drei Sechsen oder drei Vieren? Das können wir leicht ausrechnen:
- Die Wahrscheinlichkeit, mit einem Würfel eine Sechs zu werfen, ist genau 1/6.
- Die Wahrscheinlichkeit, mit drei Würfeln drei Sechsen zu werfen, ist dann 1/6 * 1/6 * 1/6 = 1/216, also doch recht gering. Umgekehrt ist die Wahrscheinlichkeit, mit drei Würfeln nicht drei Sechsen zu werfen, sehr hoch, nämlich 1 - 1/216 oder 99,54%.
So weit alles klar? Dann kommen wir nun wieder zur Entropie. Wenn wir drei Sechsen würfeln, so ist ein hochgeordneter Zustand entstanden, ein entropiearmer Zustand. Würfeln wir dagegen irgendwelche anderen Zahlen, beispielsweise eine Eins, eine Vier und eine Fünf, so können wir diesen Zustand als eher ungeordnet und entropiereich betrachten.
Ein Mathematiker müsste jetzt natürlich einwenden, dass die Wahrscheinlichkeit, eine 1, eine 4 und eine 5 zu würfeln, genau so groß ist wie die Wahrscheinlichkeit, dreimal die 6 zu würfeln.
Das ist völlig richtig, aber wenn wir Ergebnisse wie 1 - 1 - 1, 2 - 2 - 2, ... , 6 - 6 - 6 als "entropiearm" einstufen und Ergebnisse wie 1 - 2 - 1, 1 - 2 - 3, 2 - 1 - 4 und so weiter als "entropiereich", dann übersteigt die Zahl der "entropiereichen" Zustände die der "entropiearmen" bei Weitem.
Wir halten also fest:
Die Wahrscheinlichkeit, dass spontan ein entropiearmer Zustand entsteht, ist äußerst gering! Die Wahrscheinlichkeit, dass ein entropiereicher Zustand entsteht, ist dagegen recht groß.
Das Teilchen-Beispiel
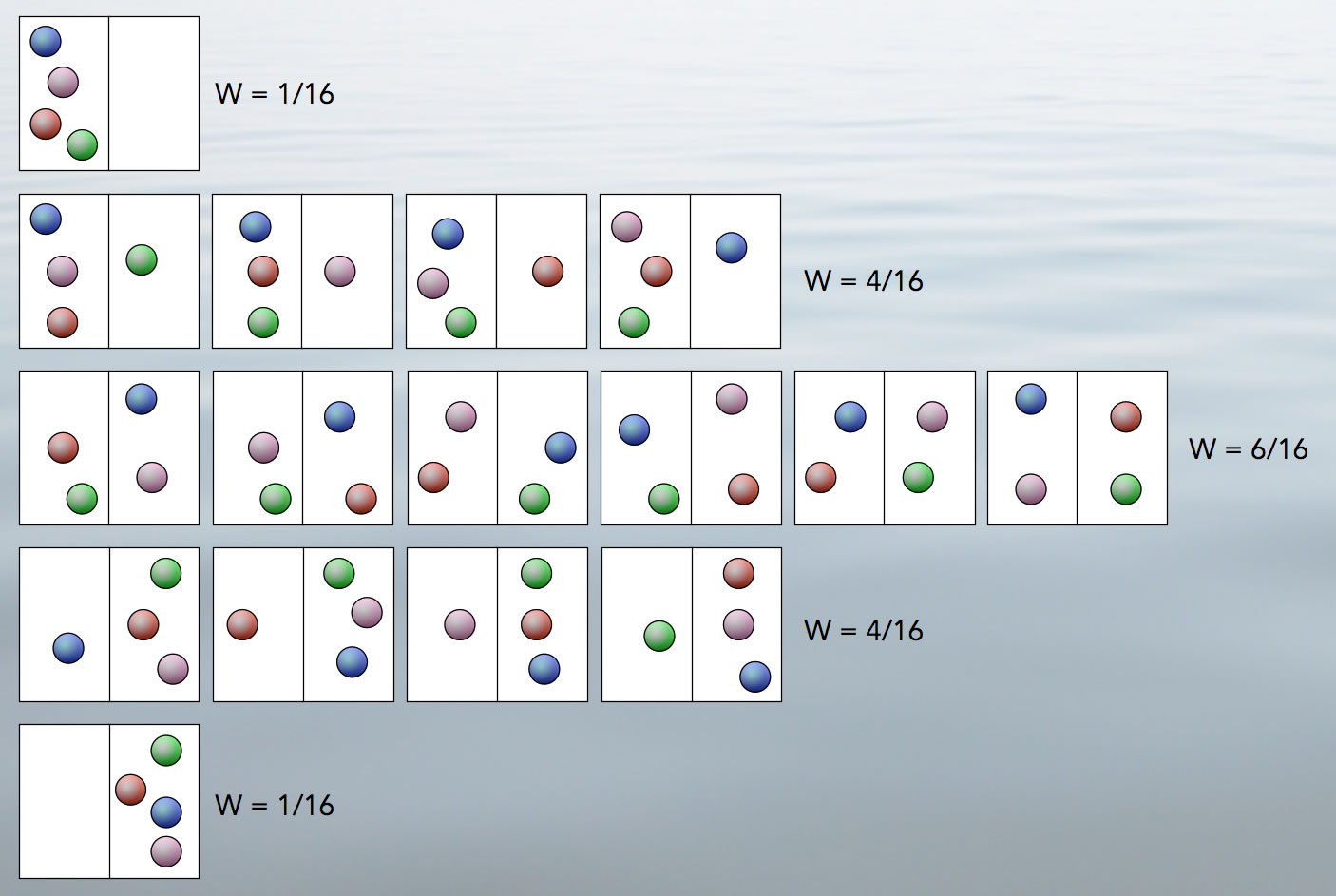
Hier noch ein Beispiel aus der Physik bzw. der physikalischen Chemie. Wir denken uns einen Raum, der in zwei gleich große Hälften unterteilt ist, eine linke und eine rechte. In diesem Raum befinden sich vier Kugeln, zunächst alle auf der linken Hälfte. Jede Kugel hat eine andere Farbe, so dass wir die Kugeln unterscheiden können. Dann gibt es genau eine Möglichkeit für die Verteilung bzw. den Makrozustand "4 links / 0 rechts".
Für den Makrozustand "3 links / 1 rechts" gibt es bereits vier verschiedene Mikrozustände, und für den Makrozustand "2 links / 2 rechts" haben wir sogar sechs verschiedene Mikrozustände. Dann gibt es noch die Makrozustände "1 links / 3 rechts" mit wieder vier Mikrozuständen und "0 links / 4 rechts" mit nur einem Mikrozustand. Insgesamt haben wir jetzt 16 dieser Mikrozustände, und mit diesem Wissen kann man jetzt die Wahrscheinlichkeit für einen der fünf Makrozustände berechnen, nämlich je 1/16 für "4 links / 0 rechts" und "0 links / 4 rechts", je 4/16 für "3 links / 1 rechts" und "1 links / 3 rechts" sowie 6/16 für "2 links / 2 rechts".
Der Makrozustand mit der höchsten Wahrscheinlichkeit ist also der mittlere mit den sechs Mikrozuständen. Hier ist die Entropie des Systems aus vier Kugeln am höchsten. In den beiden extremen Makrozuständen "4 links / 0 rechts" und "0 links / 4 rechts" ist die Entropie dagegen am geringsten - hier befinden sich quasi "alle Tassen im Schrank", was im Alltag ja auch ein hochgeordneter Zustand ist.
Entropie und Diffusion
Jetzt sollte es auch dem und der Letzten klar sein, wieso ein Konzentrationsunterschied zu einem Konzentrationsausgleich durch Diffusion führt. Der Zustand des Konzentrationsunterschiedes ist ein entropiearmer "unwahrscheinlicher" Zustand, während der Zustand des Konzentrationsausgleichs ein entropiereicher "wahrscheinlicher" Zustand ist. Durch die ungerichtete zufällige Bewegung der Teilchen (BROWNsche Molekularbewegung) stellt sich dieser wahrscheinliche Zustand mit der Zeit quasi von selbst ein.
Entropie und Wahrscheinlichkeit
Mit der folgenden Formel wird der Zusammenhang zwischen Entropie und Wahrscheinlichkeit W bzw. Anzahl der Mikrozustände eines Makrozustandes beschrieben:
S = kB * ln(W)
Die Entropie S berechnet sich aus dem natürlichen Logarithmus der Zahl der möglichen Mikrozustände W eines Systems. kB ist eine Naturkonstante, die nach ihrem "Erfinder" Ludwig Boltzmann (1844-1906) als Boltzmann-Konstante bezeichnet wird. Sie hat einen sehr unanschaulichen Wert von 1,380649 * 10-23 J/K, dabei ist K nichts anderes als die Maßeinheit Kelvin für die absolute Temperatur.
Der Makrozustand "4 links / 0 rechts" hat nur einen Mikrozustand, also ist W = 1 und S = 0, denn der natürliche Logarithmus von 1 ist nun mal 0. Die Entropie dieses Makrozustandes ist also minimal.
Der Makrozustand "2 links / 2 rechts" hat dagegen sechs Mikrozustände, also ist W = 6. Der natürliche Logarithmus von 6 ist 1,79. Die Entropie dieses Makrozustandes hat also den Wert 2,47379 * 10-23 J/K, was aber nicht sehr anschaulich ist. Sagen wir mal so: Die Entropie des Makrozustandes mit sechs Mikrozuständen ist jetzt deutlich größer als die des Makrozustandes mit nur einem Mikrozustand.
Entropie und Wahrscheinlichkeit
Diejenigen Zustände, die wahrscheinlicher sind, haben auch die größte Entropie. Entropiereicher Zustand = wahrscheinlicher Zustand.
Entropie und Chemie Studium
Der letzte Abschnitt dieser Seite richtet sich an die Experten unter Ihnen, die vielleicht schon Biologie oder Chemie studieren.
Aus chemischer Sicht versteht man unter der Entropie eines Stoffes die Wärmemenge Q, die er beim Erwärmen vom absoluten Nullpunkt (0 K) bis zur aktuellen Temperatur aufgenommen hat.
S = Qm / T
Qm ist dabei die von einem Mol des Stoffes aufgenommene Wärmemenge und T ist die absolute Temperatur in Kelvin. Ist der Druck konstant, stimmt Qm mit der Enthalpieänderung ΔH überein [2]. Die Einheit der Entropie S ist daher J * K-1 * mol-1.
Um die Reaktionsentropie ΔS zu ermitteln, verfährt man ähnlich wie bei der Ermittlung der Reaktionsenthalpie: Man berechnet die Gesamtentropie der Produkte und subtrahiert davon die Gesamtentropie der Edukte.
Haben die Produkte eine höhere Gesamtentropie als die Edukte, ist ΔS positiv, und der Term T * ΔS der Gibbs-Helmholtz-Gleichung wird negativ.
Quellen:
- Römpp Chemie-Lexikon, 9. Auflage 1992
- Binnewies et al., Allgemeine und anorganische Chemie, 3. Auflage, Springer-Verlag 2016.